Hopf argument | Pengfei's Notes

4. (Notes from the paper Stable ergodicity for partially hyperbolic attractors with negative central exponents)
Let $f\in\mathrm{Diff}^1(M)$ and $L$ be a partially hyperbolic attractor. Then there exists a $C^1$ neighborhood $\mathcal{U}\ni f$ such that every $g\in\mathcal{U}$ possesses a partially hyperbolic attractor $L_g$ near $L$ . Moreover assume $f_n\in\mathrm{Diff}^2(M)\to f\in\mathrm{Diff}^2(M)$ with Gibbs u-states $\mu_n$ on $L_n$ , then any weak limit is a Gibbs u-state on $L$ .

Let $\mu$ be an ergodic Gibbs u-state with negative central Lyapunov exponents. Then there exist an open set $U$ such that $\mu(U\Delta B(\mu))=0$ . The analog doesn’t hold for Gibbs u-states with positive central Lyapunov exponents, since the stable and unstable directions play different roles in dissipative systems.
Proof. We build a magnet $K$ over $A_r\cap F^u(x,\delta)$ with fiber $W^s(\cdot,r)$ . Then every nearby point $y\in L$ with Birkhoff-regular plaque $F^u(y,2\delta)$ , the intersection $F^u(y,2\delta)\cap K$ has positive leaf volume, and some point in there must be Birkhoff-regular, say $p\in W^s(q,r)$ for some $q\in A_r\cap F^u(x,\delta)$ . Then Hopf test: for any $z\in F^u(y,2\delta)$ , $\phi_-(z)=\phi_-(p)=\phi_+(p)=\phi_+(q)=\phi_-(q)=\phi_-(x).$ So all Birkhoff-regular plaques lie in the same ergodic omponent.

Moreover suppose $\mu$ is the unique Gibbs u-state of $(f,L)$ . Then there exists a $C^2$ neighborhood $\mathcal{U}\ni f$ such that for every $g\in\mathcal{U}$ , $(g,L_g)$ possesses a unique Gibbs u-state $\mu_g$ . Moreover $\mu_g$ has only negative central Lyapunov exponents and $\mu_g\to \mu$ as $g\to f$ . So we say $(f,L,\mu)$ is stably ergodic. Since all these measures are hyperbolic, further analysis shows that $(f,L,\mu)$ is indeed stably Bernoulli.

The key property they listed there is: for every $\delta>0$ , there exists $r>0$ and $\epsilon>0$ depending continuously of $f$ such that

– for every regular point $x$ with $\chi(x)\cap[-\delta,\delta]=\emptyset$ , the frequency of times $n$ such that the size of local Pesin manifolds at $f^nx$ is larger than $r$ is larger than $\epsilon$ .

– Moreover, for every ergodic hyperbolic measure $\mu$ with $\chi(\mu)\cap[-\delta,\delta]=\emptyset$ , theand hence the set $A_r$ of points with large Pesin manifolds has positive measure: by Kac’s formula, $\displaystyle \mu(A_r)=\int\frac{1}{n}\sum_{0\le k < n}1_{A_r}(x)d\mu\ge \epsilon$ .

3. In the continued paper here fundamental domains have been found for many invariant subsets, in particular for the set of (Birkhoff) heteroclinic points $H_f(\mu,\nu)=B(\mu,f)\cap B(\nu,f^{-1})$ (see Theorem 3.2 there, where $\mu\neq \nu$ ). It is unknown if the argument can be carried out to the set of (Birkhoff) homoclinic points $H_f(\mu)=B(\mu,f)\cap B(\mu,f^{-1})$ (for general invariant but nonergodic measure $\mu$ ). 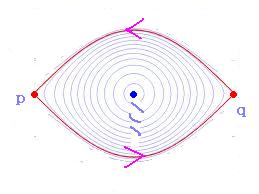Here is an example where there does exist a fundamental domain. Consider a flow on the plate $D$ with spiraling source $o$ in the center and two saddles $p,q$ at the corners.

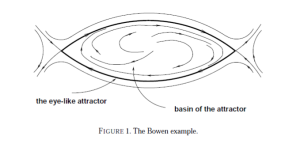
The second picture is from here, and is called Bowen eye-like attractor. Suppose the dynamics is symmetric and $V_f(x)=\mu=\frac{\delta_p+\delta_q}{2}$ for every $x\in D^o\backslash\{o\}$ , where $f$ is the time-1 map. Then it is easy to see that there exists a fundamental domain $E$ of $B(f,\mu)$ . We can blow up the center, identify the corresponding boundaries of two copies and reverse the flow direction on the second copy. Then the subset $E$ turns out to be a fundamental domain of the set of (Birkhoff) homoclinic points $H_{\hat f}(\mu)$ .

2. Let $f:M\to M$ be a $C^2$ partially hyperbolic diffeomorphism, $\mu$ be an Absolutely Continuous, Invariant Probability measure. That is, the density function $\phi=\frac{d\mu}{dm}$ is well defined in $L^1(m)$ , and the set $E_\mu=\{x\in M:\phi(x)>0\}$ is well defined in the measure-class of $\mathcal{M}(m)$ .

It is proved (Proposition 3, here) that $E_\mu$ is bi-essentially saturated (by a density argument). Similar argument shows that every invariant subset of $E_\mu$ is also bi-essentially saturated. At that time I thought the classical Hopf argument can only claim the bi-essential $\mu$ -saturation of $E_\mu$ , and Proposition 3 might be out of the range of Hopf argument. Now it seems this is not the case if we combine some results in Gibbs $u$ -measures, which states, for example, the conditional measures $\mu_{W^u(x)}$ of $\mu$ with respect to the unstable foliation $\mathcal{W}^u$ is not only abs. cont., but also smooth: the canonical density (see here) $\rho^u_{\text{can}}(x,y)=\frac{d\mu_{W^u(x)}(y)}{dm_{W^u(x)}}$ is Holder, bounded and bounded away from zero, since ACIP is automatically a Gibbs $u$ -measure.

So let $E$ be an invariant subset of $E_\mu$ . Then Hopf argument implies that

$\mu_{W^u(x)}(E\backslash W^u(x))=0$ for $\mu$ -a.e. $x\in E$ , or equivalently,

$m_{W^u(x)}(E\backslash W^u(x))=0$ for $\mu$ -a.e. $x\in E$ (by the previous observation), and moreover

$m_{W^u(x)}(E\backslash W^u(x))=0$ for $m$ -a.e. $x\in E$ (since $\mu\simeq m$ on $E_\mu$ ).

Then a standard argument shows that $E$ is essentially $u$ -saturated. Similarly ACIP is automatically a Gibbs $s$ -measure and $E$ is essentially $s$ -saturated. This shows that $E$ is bi-essentially saturated by Hopf argument and Gibbs theory.

1. Let $W$ be a plaque of the Pesin unstable manifold of $f$ , and consider a function $\rho(x)$ with the property that $\displaystyle \frac{\rho(x)}{\rho(y)}=\prod_{k\ge1}\frac{J^u(f,f^{-k}y)}{J^u(f,f^{-k}x)}$ for all $x,y\in W$ , and the normalizing condition $\int_W \rho\,dm_W=1$ . Let $\mu=\rho m_W$ be the induced probability on $W$ . It is conditionally invariant under $f$ : Consider its pushforward $f\mu=\eta m_{fW}$ . Then: $\mu(A)=(f\mu)(fA)=\int_{fA}\eta(y) dm_{fW}(y)=\int_{A}\eta(fx)\cdot J^u(f,x)dm_W(x)$ for any $A\subset W$ . Hence $\rho(x)=\eta(fx)\cdot J^u(f,x)$ . In particular $\displaystyle \frac{\eta(fx)}{\eta(fy)}=\frac{\rho(x)}{\rho(y)}\cdot\frac{J^u(f,y)}{J^u(f,x)}=\frac{\rho(fx)}{\rho(fy)}$ .
Then by definition, both $\rho$ and $\eta$ induce probabilities and must coincide:
$f(\rho\cdot m_W)=(\rho\circ f)\cdot m_{fW}$ . Such measures are called the leafwise u-Gibbs measures.